机器学习模型评测指标
文章目录
假定有一个二分类问题,比如判定商品是否是假货。给系统一个样本,系统将会判断该样本为“真”(Predicted positive),或“假”(Predicted Negative)。但是当然,系统的判断与真实判断(actual positive/negative)是有误差的,将原本是真的判为真,就是TP(True Positive),原本真的判为假,就是FN(False Negative),原本假的判为真,就是FP(False Positive),原本假的判为假,就是TN(True Negative)。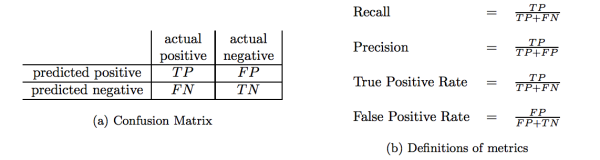
精确率(Precision)是指在所有系统判定的“真”的样本中,确实是真的占比,就是TP/(TP+FP)
召回率(Recall)是指在所有确实为真的样本中,被判为“真”的占比,就是TP/(TP + FN)
TPR(True Positive Rate)的定义和Recall定义一样
FPR(False Positive Rate), 又被称为”Probability of False Alarm”, 就是所有确实为“假”的样本中,被误判为真的样本,或者FP/(TN + FP)
F1 是为了综合考量精确率和召回率而设计的一个指标,一般公式为取P和R的 harmonic mean:2PrecisionRecall/(Precision+Recall)。
ROC=Receiver Operating Characteristic,是TPR vs FPR的曲线;与之对应的是Precision-Recall Curve,展示的是Precision vs Recall的曲线。
显而易见的,当TN=FN=0的时候,也就是我们将100%的样本都认为是“真”的,TPR=FPR=1:这就是我们“完全放水”的情形;反之,当TP=FP=0的时候,也就是我们将100%的样本都认为是“假”的时候,TPR=FPR=0,这就是“宁可错杀一万,不可放过一个”的情形。
我们在下图观察几个点。首先,FPR=0, TPR=1的那个点,可以推测FN=0, FP=0:一个错误都没有,所以是Perfect Classification。中间这条红线,我们观察TPR=FPR,所以TP(FP+TN)=FP(TP+FN),所以TP/FN = FP/TN:换言之,无论样本是真是假,我们将它们判为“真”或“假”的概率都相当,或者说,我们的猜测是完全随机的。
在红线上方,偏Perfect Classification的区域,我们认为是优于随机猜测。因为,在红线上的任意一点垂直向上的点,都有同样的FPR,但总是得到更高的TPR:在错误不变的情况下,我们的Recall变高了。反之,在红线下方的点,都认为是劣于随机猜测。
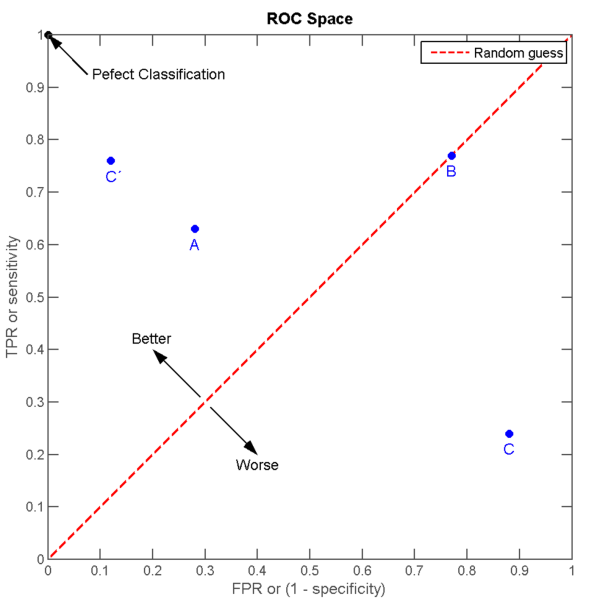
那么聪明的你一定想得到,ROC曲线下方所包围的面积越大,那么分类器的性能越优越。这个曲线下的面积,就叫做AUC(Area Under the Curve)。因为整个正方形的面积为1,所以0<=AUC<=1。同理,Precision与Recall的关系也可以画成一条曲线,就是上面的PR curve,其中,Precision随着Recall的提高而降低。
二分类问题
指标的好坏主要取决于分类器的目标。比方说,电子邮件的垃圾过滤,你是希望它更全面(查出所有的垃圾,但是会有大量有用信息也被判为垃圾)呢,还是希望它尽量精准(不要老是将有用的邮件判为垃圾)呢?在这个例子里,显然,我们认为False Positive的伤害要大于False Negative:重要邮件要是被判成垃圾所造成的损失,远大于收件箱里还有一部分的垃圾邮件——前者可能会让你错过重要的工作,后者仅仅是让你在阅读的时候皱皱眉头。在这种情况下,我们会认为Precision的指标会比较重要,或者反应在ROC图上,FPR尽量的小——自然,在保证FPR的基础上,Recall依然还是重要的——毕竟用户购买的是垃圾过滤,如果只是过滤了1条垃圾但是Precision=100%,这样的东西看起来也没什么用——那么综合起来,我们也可以通过ROC的AUC来进行比较,面积较大的代表同样的FPR下面,recall比较高。
但是,ROC的曲线——如上面几位已经说过——有数据均衡的问题。在数据极度不平衡的情况下,譬如说1万封邮件中只有1封垃圾邮件,那么如果我挑出10封,50封,100,。。封垃圾邮件(假设全部包含真正的那封垃圾邮件),Recall都是100%,但是FPR分别是9/9999, 49/9999, 99/9999(数据都比较好看:FPR越低越好),而Precision却只有1/10,1/50, 1/100 (数据很差:Precision越高越好)。所以在数据非常不均衡的情况下,看ROC的AUC可能是看不出太多好坏的,而PR curve就要敏感的多。(不过真实世界中,垃圾邮件也许与你的有用的邮件一样多——甚至比有用的还更多。。。)
其次是搜索问题
搜索问题其实是一个排序问题,但我们往往会定义Precision@Top K这样的指标,即正确的答案有没有被排在Top K中,如果是的话,就相当于判断为“真”,反之则为“否”。这样搜索问题就转化为了一个二分类问题,唯一的问题是,这是一个典型的数据不均衡的case。很显然,所有的候选集的数量是非常巨大的,但是K的数量不会很大(比如Top 10, Top 20)。
所以,在这个问题中,我们会主要看Precision-Recall curve。
更重要的是,一般而言,人们看搜索结果都不会太有耐心,所以希望Top K中的有用信息尽量多,换言之,Precision@Top K的指标,是最核心的。我们再考虑一个任务,机器阅读理解(Machine Reading Comprehension, MRC),机器阅读一篇文章以后人类向它提问,由机器回答。这时候,所谓的Precision,是指机器回答的答案中,正确的比例。但是在这个任务中,Recall同样重要:机器也有可能回答不出来问题,但是“回答不出”,其实和“回答错误”是没有差别的。在这样的任务中,我们希望能够公平的Balance Precision和Recall的一个数字,所以我们认为F1 Score是一个好的衡量指标。
然而如果我们的问题是多分类的问题,实际上这些指标就不适合了,我们需要看的是Confusion Matri: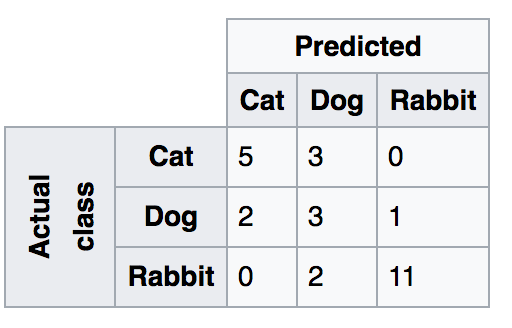
在上图中,对于某一类别(比如猫)而言,错误会分为被误判成狗或误判成兔子两种情形,共记9种不同的类别,其中三类(对角线上的元素)是分类正确的。显然,仅仅用TP/TN/FP/FN这四类已经不足以分析这样的问题了。当然,指标也不仅限题主所列这几种,这里就不展开了。需要提一下的是,很多时候,能否有效的分析实验结果,比单纯算法上几个点的差异,对结果的影响来的大得多。在没有指定具体情况的时候谈指标,是没有任何意义的。
需要注意的几点
- 在正负样本分布得极不均匀(highly skewed datasets)的情况下,PRC比ROC能更有效地反应分类器的好坏。
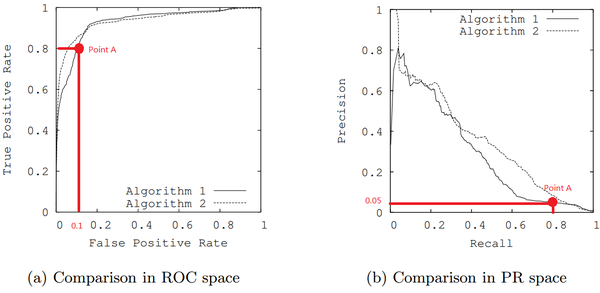
具体分析图2.
单从图a看,这两个分类器都接近完美(非常接近左上角)。图b对应着相同分类器的PR space。而从图b可以看出,这两个分类器仍有巨大的提升空间。
那么原因是什么呢? 通过看Algorithm1的点 A,可以得出一些结论。首先图a和b中的点A是相同的点,只是在不同的空间里。因为TPR=Recall=TP/(TP+FN),换言之,真阳性率(TPR)和召回率(Recall)是同一个东西,只是有不同的名字。所以图a中TPR为0.8的点对应着图b中Recall为0.8的点。
假设数据集有100个positive instances。由图a中的点A,可以得到以下结论:TPR=TP/(TP+FN)=TP/actual positives=TP/100=0.8,所以TP=80
由图b中的点A,可得:Precision=TP/(TP+FP)=80/(80+FP)=0.05,所以FP=1520
再由图a中点A,可得:
FPR=FP/(FP+TN)=FP/actual negatives=1520/actual negatives=0.1,所以actual negatives是15200。
由此,可以得出原数据集中只有100个positive instances,却有15200个negative instances!这就是极不均匀的数据集。直观地说,在点A处,分类器将1600 (1520+80)个instance分为positive,而其中实际上只有80个是真正的positive。 我们凭直觉来看,其实这个分类器并不好。但由于真正negative instances的数量远远大约positive,ROC的结果却“看上去很美”。所以在这种情况下,PRC更能体现本质。
结论: 在negative instances的数量远远大于positive instances的data set里, PRC更能有效衡量分类器的好坏。
- PR曲线会面临一个问题,当需要获得更高recall时,model需要输出更多的样本,precision可能会伴随出现下降/不变/升高,得到的曲线会出现浮动差异(出现锯齿),无法像ROC一样保证单调性。学术论文在假定正负样本均衡的时候多用ROC/AUC,实际工程更多存在数据标签倾斜问题一般使用F1